
Явление SCP-1941 (фото предоставлено ЛОРА). Чёрная область, напоминающая сеть, является результатом продолжающегося строительства.
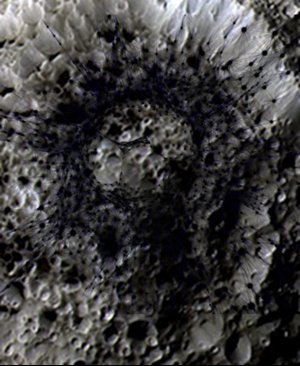
Деталь отдельного узла и его раскопки. Сеть самоподобна: отдельные узлы напоминают сеть в целом. Изображённое здесь является эквивалентом единичного узла на предыдущей фотографии. Это изображение сделано на дальнем пределе разрешающей способности ЛОРА (кратер имеет примерно 50 м в ширину).
Объект №: SCP-1941
Класс объекта: Евклид
Особые условия содержания: Ввиду своего расположения SCP-1941 на сегодняшний день является несодержащимся. Высочайшим приоритетом является развитие передовых лунных орбитальных разведывательных аппаратов для продолжения отслеживания процесса, а также организация лунной экспедиции с целью добыть образец для исследования. На данный момент это явление не видно с Земли, что делает прикрытие ненужным1.
Описание: SCP-1941 - обозначение явления, впервые обнаруженного 28 мая 2000 года, когда было замечено падение объекта, сочтённого небольшой кометой, в 500 км к юго-востоку от кратера Джексона в северном полушарии обратной стороны Луны. С момента его обнаружения появились признаки быстро развивающейся индустриальной активности и экспоненциального разрастания.
Разрешающая способность используемого в настоящее время лунного орбитального разведывательного аппарата (ЛОРА) недостаточна, чтобы точно определить, чем вызваны вышеупомянутые события. Тем не менее, аномально высокие температуры и результаты спектроскопии позволяют предположить, что имеют место добыча ископаемых открытым способом, их переработка и производство каких-то изделий. Кроме того, обнаружена нейтринная активность, соответствующая управляемой реакции термоядерного синтеза.
Было высказано предположение, что столкнулось с Луной и стало причиной SCP-1941 чужеродное устройство, использующее сверхсовременные технологии. Такое устройство (известное в качестве зонда фон Неймана) способно использовать имеющееся в окружающей среде сырьё для создания своих копий. Произведя достаточное количество экземпляров, оно может переключиться на какую-то более долгосрочную цель.
В течение десяти лет с момента обнаружения охватываемая явлением площадь выросла в 3,5 раза, в течение 7 лет ожидается удвоение скорости. В настоящее время явление охватывает площадь в 250 000 км2 (6% поверхности Луны, что примерно равно площади Великобритании). Если оно продолжит распространяться с той же скоростью, то станет видимым с Земли в августе 2023 года, а к 2040 году покроет всю поверхность Луны.
Приложение: В июне 2002 года были впервые обнаружены сигналы с места действия явления. Они состояли из вспомогательной лингвистической программы, определяющей небольшой математический словарь, с последующим предоставлением специфического числа и запроса на определение его простых множителей. В настоящее время неизвестно, какие последствия будет иметь передача или непередача ответа. К сожалению, заданное число столь велико, что решение задачи его разложения на множители любыми обычными средствами на данный момент не представляется возможным.
Неизвестно, обусловлена ли сложность этой математической задачи тем, что она является неким тестом на интеллект, либо же тем, что создавшая SCP-1941 цивилизация резко переоценила способности человечества. Существует возможность, что она разработана для измерения уровня развития цивилизации и оценки сопротивления, которое она может оказать в случае, если намерения SCP-1941 на самом деле враждебны.
Ниже приведено выражение для данного числа:
Последние события: В марте 2014 года в том, что считалось помехами основного канала, было обнаружено второе сообщение. Анализ второго сообщения при помощи ранее установленного математического словаря позволяет предположить, что передача его простых множителей будет означать прекращение лунного явления. Было высказано предположение, что SCP-1941 запрограммирован на выключение, если соседняя цивилизация достаточного уровня развития сочтёт его деятельность нежелательной.
Это обстоятельство делает ещё более значимым решение задачи, полученной в первом сообщении. Было проведено исследование возможности использования вычислительных мощностей SCP-155 (SCP-155 представляет собой компьютер, способный производить асимптотическое количество вычислений в конечные отрезки времени), а также сопутствующих рисков (см. документацию по SCP-155).
Были проведены оценки количества энергии, которое будет высвобождено SCP-155 во время этой попытки, а также расчёт того, потребуется ли его перемещение за пределы Земли для защиты от события класса WK (или стерилизации всей жизни на планете). Нижняя граница предполагаемого количества энергии составляет 4,2 х 1018 Дж, что считается приемлемым (это примерно эквивалентно ядерному взрыву мощностью в одну гигатонну). Однако верхняя граница составляет 3,1 х 1044 Дж - приблизительное количество энергии, выделяемой в среднем сверхновой звездой. В настоящее время ведётся исследование по уточнению этих границ.
Математическое дополнение:
Второе сообщение выглядит следующим образом:
Интерпретация данного выражения приведена ниже:
(1): Определение функции , которая образует простые множители целого числа.
(2): Определение чрезвычайно большого числа .
(3): Условие, при котором простые множители пустого множества образуют основание натурального логарифма е (интерпретировано как продолжение экспоненциального роста), а простые множители большого числа дает 0 (интерпретировано как прекращение роста).
Верхние и нижние границы:
Нижняя граница оценивается исходя из предположения, что, поскольку число стремится к бесконечности, будет иметь примерно простых множителей. Верхняя граница оценивается исходя из предположения, что число представляет собой вырожденный случай и само является простым числом.
« SCP-1940 | SCP-1941 | SCP-1942 »

